Résolution de l'équation d'onde en 2-D par différences finies

Théorie

Nous résolvons cette fois l'équation
où z(x,y,t) désigne l'amplitude d'une onde et v est la vitesse de propagation dans le milieu considéré.

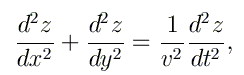
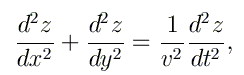
Nous discrétisons les espaces x et y suivant des intervalles Δx et Δy, et le temps t suivant des intervalles Δt. En utilisant les expressions discrétisées des dérivées secondes, l'équation précédente se transforme comme

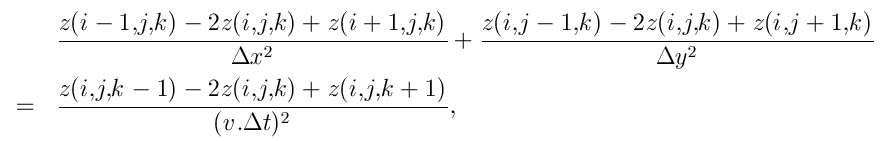
où z(i,j,k) désigne la valeur de y(x,y,t) en x=i.Δx, y=j.Δy et t=k.Δt.

Cette équation peut encore se mettre sous-la forme

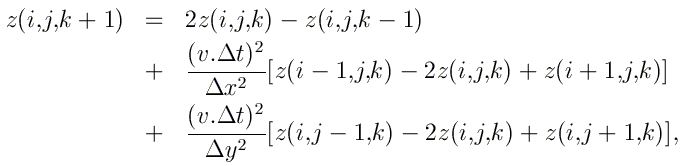
ce qui permet de calculer les amplitudes de l'onde au temps (k+1).Δt si l'on connait les amplitudes en k.Δt et (k-1).Δt.

Le choix idéal pour Δt est ici donné par

Dans ce processus numérique, le passage de l'onde d'une cellule (i,j) à une cellule (i±1,j±1) doit en effet se faire en deux temps [(i,j)→(i±1,j)→(i±1,j±1)]. Prendre un Δt plus grand conduit l'onde à s'écraser et la méthode devient instable. Prendre un Δt plus petit rend la méthode essentiellement plus lente.

Mise en pratique

Nous allons résoudre cette équation pour une surface carrée de côtés Lx=Ly=100 m. Le nombre de cellules suivant x et y sera choisi comme Nx=Ny=140.

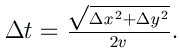
Nous placerons une source sinusoïdale d'amplitude 1 et de fréquence ν = 2 Hertz en (Lx/3,Ly/2). L'amplitude de l'onde en i=Nx/3 et j=Ny/2 sera donc modifiée à chaque étape comme

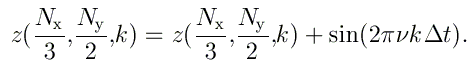
Finalement, le milieu sera caractérisé par une vitesse de propagation v de 10 m/s.

  1. Vous allez calculer dans un premier temps les amplitudes z(x,y,t) pour des temps supérieurs. Pour représenter graphiquement vos résultats, vous utiliserez les sous-routines données plus loin.

    Pour la première étape de propagation (de t=0 à t=Δt), on pose à nouveau que z(i,j,-1)=z(i,j,1). Ceci permet d'écrire

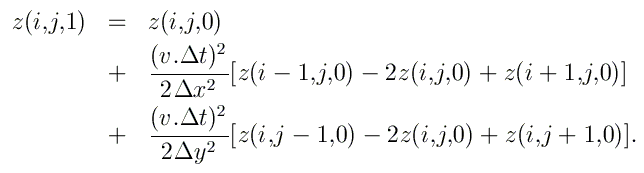
    Les étapes de propagation suivantes se font alors suivant l'équation donnée précédemment. A ce stade, on pose toujours que

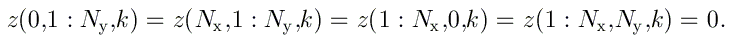
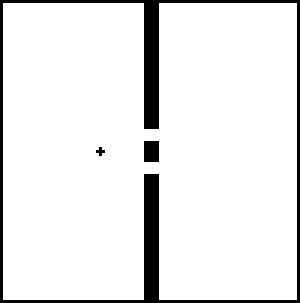
  2. Après avoir réalisé l'étape précédente, vous allez introduire une double fente dans le système. Celle-ci sera placée comme dans le schéma suivant.

    L'extension de cette fente suivant x correspond à l'intervalle [(10/21)Lx,(11/21)Lx]. Les deux trous suivant y correspondent aux intervalles [(43/100)Ly,(46/100)Ly] et [(54/100)Ly,(57/100)Ly]. On introduit cette fente dans nos simulations en appliquant à chaque étape un "masque de zéros" aux points associés avec cette fente. Ceci introduit en effet une réflection des ondes incidentes, exactement comme aux limites du système.

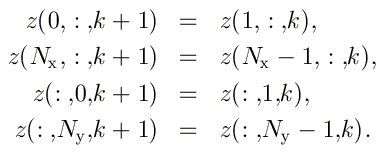
  3. Pour supprimer les réflections aux bords du système, on peut généraliser l'idée utilisée en une dimension. On appliquera donc les conditions frontières suivantes:

    Les ondes sont-elles encore réfléchies ?

    Ces relations, déterminées heuristiquement à partir de nos observations pour le cas unidimensionnel, définissent des "conditions frontières absorbantes d'ordre 1" (on peut les appliquer telles quelles lorsque Δt = sqrt(Δx2+Δy2) / 2v. Elles sont surtout efficaces pour des ondes ayant une incidence perpendiculaire aux limites du système. Pour des ondes plus inclinées, une certaine réflection apparaît. Il existe des "conditions frontières absorbantes d'ordre 2" ainsi que d'autres méthodes plus efficaces en électromagnétisme.

A remettre ...

Pour ce TP, vous devez me remettre:

Voici le Makefile à utiliser avec le gfortran (le programme principal doit s'appeler Wave2D.f90).

Sous-routine Map pour une représentation graphique de fonctions z=z(x,y)

Afin de représenter graphiquement vos résultats, vous pouvez utiliser la routine Map. Celle-ci vous permet de visualiser une fonction z=z(x,y) en faisant simplement call Map(list_x, list_y, list_z). Vous devez pour cela inclure use MapPack dans les parties de vos programmes qui utilisent Map. Vous trouverez plus de détails sur son utilisation dans les commentaires préliminaires du fichier.

Pour obtenir une image animée, vous devez faire

call Map(list_x, list_y, list_z, keep=.true., refresh=.false.)

lors de la première utilisation et

call Map(list_x, list_y, list_z, keep=.true., refresh=.true.)

ensuite.

Finalement, pour stabiliser l'échelle de gris, vous pouvez ajouter les arguments suivants:

zmin=-0.75_r, zmax=0.75_r.

Sous-routine PgMap pour une sortie PostScript de fonctions z=z(x,y)

Afin d'obtenir une sortie PostScript d'une fonction z=z(x,y), vous pouvez utiliser la routine PgMap. Celle-ci s'utilise de manière similaire à Map. Pour représenter une fonction z=z(x,y), il suffit en effet de faire call PgMap(list_x, list_y, list_z). Vous devez pour cela inclure use PgMapPack dans les parties de vos programmes qui utilisent PgMap. Vous trouverez plus de détails sur son utilisation dans les commentaires préliminaires du fichier.