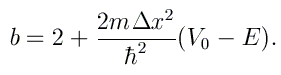
Calcul de la transmission électronique à travers une barrière de potentiel

Théorie

Nous allons appliquer la technique des fractions continues pour calculer la transmission d'états électroniques à travers une barrière de potentiel V(x). Cette barrière est caractérisée par une longueur L et discrétisée en x=i.Δx, où i va de 1 à N (Δx=L/N).

Nous posons que les régions d'incidence et de transmission sont caractérisées par un potentiel constant V₀. Les coefficients b_i rencontrés dans la technique des fractions continues prennent alors la valeur constante

Les solutions de l'équation de Schrödinger dans ces deux régions vérifient par ailleurs

pour des états Ψ⁺=A e^ikx se propageant vers la droite, et

pour des états Ψ^-=B e^-ikx se propageant vers la gauche.

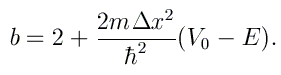
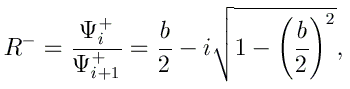
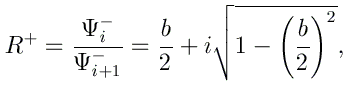
Pour le problème de diffusion, nous posons l'existence d'un état sortant dans la région de transmission. Cela revient à poser cette fois

On peut alors appliquer la relation de récurrence

avec

pour calculer R₀ (la relation de récurrence est ainsi appliquée pour chaque point i de la barrière de potentiel). Un dernier effort permet de calculer

L'état électronique ainsi obtenu dans la région d'incidence peut alors s'exprimer comme la somme d'un état incident Ψ⁺=A e^ikx et d'un état réfléchi Ψ^-=B e^-ikx. Ceci permet d'écrire

de sorte que le coefficient de réflexion R est donné par

où les coefficients R_-1, R^- et R⁺ sont connus.

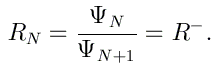
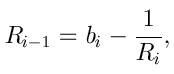
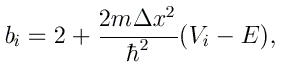
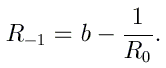
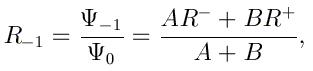
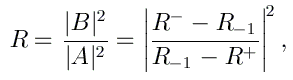
Le coefficient de transmission T est finalement calculé par

Mise en pratique

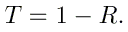
Le potentiel considéré sera celui pour lequel nous avons calculé la structure de bandes:

où V₁ = 1 eV et L = 0.4336 nm.

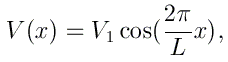
Comme précédemment, nous discrétisons le motif de base [0, L] de ce potentiel avec N=40 points. Les régions d'incidence et de transmission sont caractérisées par un potentiel V₀ de 0 eV.

En appliquant la méthode des fractions continues, calculez le coefficient de transmission T(E) pour des énergies E allant de 0 à 10 eV (par pas de 0.01 eV). Vous représenterez le coefficient de transmission T(E) graphiquement.
Généralisez votre programme de manière à calculer le coefficient de transmission T(E) correspondant à 1, 2, 4, 8, 16, 32, 64 et 128 cellules de base du potentiel (pour des énergies E comprises entre 0 et 10 eV).
Vous représenterez ces 8 courbes sur le même graphique.
Comment reliez-vous les résultats obtenus autour de 2 et 8 eV avec la structure de bandes calculée pour le méme potentiel ?
Représentez en échelle logarithmique le coefficient de transmission T(E), pour E=2 eV (milieu du gap) et un nombre de cellules allant de 1 à 64.
Commentez vos observations (loi de décroissance de la transmission dans le gap + problème rencontré à grande distance).
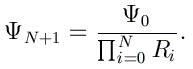
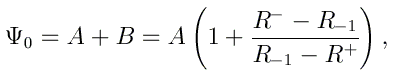
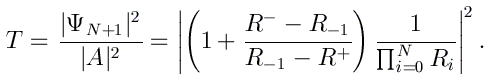
Une autre manière de calculer le coefficient de transmission consiste à exprimer Ψ_N+1 comme Puisque on montre facilement que le coefficient de transmission peut également s'obtenir par Comparez le résultat précédent (coefficient de transmission pour E=2 eV en fonction du nombre de cellules) avec celui obtenu par cette deuxième relation.

A remettre ...

Pour ce TP, vous devez me remettre:

le listing de votre programme
tous les graphiques demandés
vos réponses aux questions

Sous-routine Plot pour une représentation graphique de fonctions y=y(x)

Afin de représenter graphiquement vos résultats, vous pouvez utiliser la routine Plot. Celle-ci vous permet de visualiser une ou plusieurs fonctions y=y(x) en faisant simplement call Plot(list_x, list_y). Vous devez pour cela inclure use PlotPack dans les parties de vos programmes qui utilisent Plot. Vous trouverez plus de détails sur son utilisation dans les commentaires préliminaires du fichier.

Programme Plot.py pour une représentation graphique de fonctions y=y(x)

Si vous connaissez le Python, vous pouvez encore faire python Plot.py Plot.dat (Python 2.7). Vous trouverez dans le fichier Plot.dat un exemple de format à respecter.

Sous-routine PgPlot pour une sortie PostScript de fonctions y=y(x)

Afin d'obtenir une sortie PostScript de fonctions y=y(x), vous pouvez utiliser la routine PgPlot. Celle-ci s'utilise de manière similaire à Plot. Pour représenter une ou plusieurs fonctions y=y(x), il suffit de faire call PgPlot(list_x, list_y). Vous devez pour cela inclure use PgPlotPack dans les parties de vos programmes qui utilisent PgPlot. Vous trouverez plus de détails sur son utilisation dans les commentaires préliminaires du fichier.