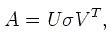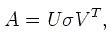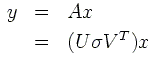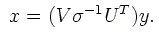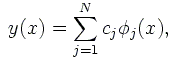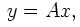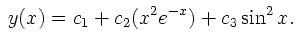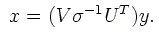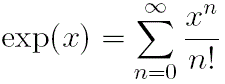Ajustement linéaire général par une décomposition SVD

Théorie

La décomposition SVD d'une matrice rectangulaire A(M,N) est donnée par l'expression


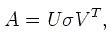
où σ est une matrice diagonale qui contient les valeurs singulières de A. U et V sont deux matrices orthogonales. Cette définition généralise en quelque sorte la décomposition spectrale A=X Λ X-1 d'une matrice carrée. La dimension de σ vaut ici le minimum de M et N. Lorsque M > N, on a donc des matrices U(M,N), σ(N,N) et V(N,N).

Ayant posé cela, on peut résoudre le système

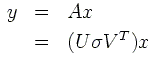en prenant simplement

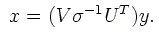
Dans cette expression, σ-1 est une matrice diagonale dont les éléments sont σi-1 lorsque σi≠0 et 0 sinon. Le x fourni par cette expression minimise la grandeur ||y-Ax||2. Parmi tous les x réalisant une minimisation équivalente de ||y-Ax||2, celui obtenu en prenant σi-1=0 lorsque σi=0 a la norme la plus petite.

Dans le problème d'ajustement linéaire qui nous intéresse, on souhaite modéliser un ensemble de M points (xi,yi) par une expression

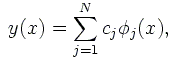où les fonctions φj(x) sont fixées et les coefficients cj doivent être déterminés afin de représenter au mieux le nuage de points. On a donc un système de M équations à N inconnues, qui peut s'écrire sous la forme

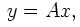
où le vecteur y(1:M) contient les yi, la matrice A(M,N) contient les éléments Aij=φj(xi) et le vecteur x(1:N) contient les coefficients cj. On utilisera la technique SVD pour résoudre ce système d'équations.

Exercices

  1. On souhaite modéliser les points (xi,yi) représentés dans le graphique suivant par une expression du type


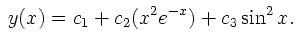
    Le but de l'exercice est de déterminer les coefficients c1, c2 et c3 en appliquant la technique SVD.
    Les fonctions de base à considérer seront φ1(x)=1, φ2(x)=x2e-x et φ3(x)=sin2x.


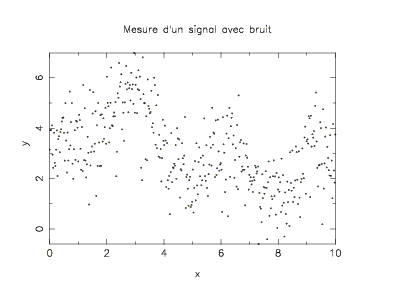
    Dans le cas présent, nous avons M=400 points (xi,yi) à reproduire et N=3 fonctions de base.

    Vous devez donc construire le vecteur y(1:M) qui contiendra les yi, la matrice A(M,N) qui contiendra les φj(xi), calculer sa décomposition en valeurs singulières et utiliser la relation


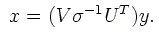
    Le vecteur x(1:N) ainsi obtenu contiendra les coefficients cj.

    Vous trouverez la liste des points (xi,yi) dans le fichier signal.dat. Une fois les coefficients cj calculés, vous représenterez les points (xi,yi) ainsi que le fit.

    Votre programme devra être général et s'appliquer pour des valeurs quelconques de M et N.

  2. Comme second exercice, vous allez comparer la fonction exponentielle exp(x) avec son développement en série de Taylor et sa décomposition SVD.

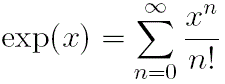
    Vous allez considérer pour cela M=250 valeurs de xi comprises entre 0 et 5. Les fonctions de base seront données par φj(x)= xj-1.
    Les coefficients cj seront soit définis par cj=1/(j-1)! (développement en série de Taylor), soit obtenus par la méthode SVD.

    Le programme devra demander la valeur de N à considérer. Vous prendrez en particulier N=2 et N=4.

    Vous devez produire deux graphiques (un pour N=2 et un pour N=4). Chaque graphique représentera pour x allant de 0 à 5 :

    • la fonction exponentielle exp(x)
    • la représentation obtenue en prenant cj=1/(j-1)! (développement en série de Taylor)
    • la représentation obtenue en prenant les cj fournis par la méthode SVD.

    Programmez de manière générale. Quels sont les avantages respectifs de chaque représentation (Taylor/SVD) ?

  3. [Optionnel] Vous pouvez généraliser l'exercice précédent et écrire un programme qui réalise ce qui suit :

    • lire un fichier contenant une fonction quelconque
    • demander à l'utilisateur d'entrer la valeur de N à considérer pour l'ajustement polynomial de cette fonction (les fonctions de base sont données par φj(x)= xj-1)
    • calculer par la méthode SVD les coefficients cj de cet ajustement
    • afficher l'expression mathématique de l'ajustement ainsi obtenu
    • produire un graphique avec la fonction originale et son ajustement polynomial
    • produire deux graphiques contenant respectivement la première et la seconde dérivée de la fonction contenue dans le fichier d'entrée (on obtient ces dérivées en dérivant analytiquement les fonctions de base utilisées pour la méthode SVD)

    Cette généralisation vous fournira un outil très utile pour la suite de votre parcours.

Sous-routine

Pour obtenir la décomposition SVD d'une matrice réelle (double précision), vous pouvez utiliser la sous-routine dgesdd de la librairie LAPACK. Cette librairie propose en effet des sous-routines optimisées pour différentes architectures. Il est fortement recommandé de l'utiliser lorsque c'est possible. La syntaxe de cette sous-routine est la suivante:

call DGESDD( JOBZ, M, N, A, LDA, S, U, LDU, VT, LDVT, WORK, LWORK, IWORK, INFO )

où JOBZ='S' pour obtenir les valeurs et vecteurs singuliers de la matrice A(M,N), LDA=M, S(1:min(M,N)) contient en sortie les valeurs singulières, U(1:M,1:min(M,N)) contient en sortie la matrice U, LDU=M, VT(1:min(M,N),1:N) contient en sortie VT, LDVT=min(M,N), WORK(1:LWORK) est un espace de travail (il s'agit d'un vecteur réel double précision), LWORK=3*min(M,N)*min(M,N)+max(max(M,N),4*min(M,N)*min(M,N)+4*min(M,N)), IWORK(1:8*min(M,N))est un autre espace de travail (il s'agit d'un vecteur entier) et INFO est un entier qui vaut 0 en sortie si tout s'est bien passé. Vous trouvez toutes ces explications au début du listing de dgesdd.

Vous pouvez utiliser dgesdd directement, sans l'inclure dans votre projet ni créer d'interface ! Il faut cependant compiler votre projet en le liant à la librairie LAPACK. La manière de faire dépend de votre compilateur. Vous trouverez les explications nécessaires sur ma page consacrée à LAPACK. On trouve facilement la routine à utiliser pour un problème donné en parcourant le site de la librairie. La manière d'utiliser cette routine est alors expliquée au début du listing.

Voici le Makefile à utiliser avec le gfortran (le programme principal doit s'appeler SVD.f90).

Remarques

  1. Dans ces exercices, mes "M et N" correspondent aux "N et M" du cours théorique. J'ai fait ce choix de notations afin d'être cohérent avec les "M et N" de la sous-routine DGESDD.
  2. En pratique, on peut annuler les valeurs singulières qui sont déjà très petites par rapport aux autres valeurs. Ces valeurs singulières participent en effet peu à la transformation directe A (elles représentent en général du bruit dans la transformation directe). Par contre, elles peuvent dominer la transformation inverse. Les annuler simplement permet de mieux filtrer le bruit dans une reconstruction.