
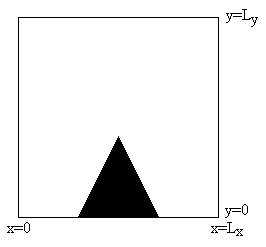
Vous utiliserez pour cela le programme GetMap.exe. Vous trouverez dans le fichier GetMap.dat un exemple du format à respecter.
Si vous connaissez le Python, vous pouvez également faire python Map.py Map.dat (Python 2.7). Vous
trouverez dans le fichier Map.dat un exemple de format à respecter.
Le temps se mesure en Fortran en faisant call cpu_time(time), où
time est un réel simple précision. On mesure des intervalles de temps dt en prenant la différence entre deux temps time1 et time2 mesurés à des endroits différents du programme.
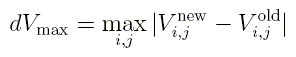
Vous utiliserez pour cela le programme GetPlot.exe. Vous trouverez dans le fichier GetPlot.dat un exemple du format à respecter.
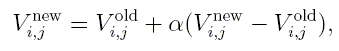
Vous représenterez simultanément les résultats obtenus pour α = 1, 1.5, 1.75 et 1.95.