Etude des oscillations d'un pendule excité

Présentation

Considérons un pendule rigide de longueur l, qui est soumis à la force gravifique et dont le point de suspension oscille comme u(t)=R sin ω t.

Le but de l'exercice est de calculer les variations de l'angle θ au cours du temps.

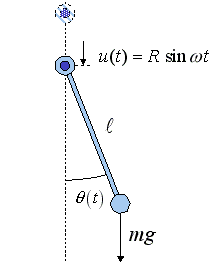
En écrivant l'équation de Newton de la masse m et en se rappelant que l est constant, on peut montrer que l'angle θ obéit à l'équation suivante:

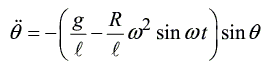
Il s'agit d'une équation différentielle du deuxième ordre. Pour pouvoir la traiter avec une routine telle que rkf45, il est nécessaire de la réduire à un système d'équations du premier ordre. Cela se fait simplement en posant:

L'équation du pendule peut alors se ramener à:

qui est un système du premier ordre.

Routines utilisées

Afin de propager numériquement les valeurs de y₁=θ et y₂=θ', nous allons utiliser les routines et modules suivants:

rkf45.f90, une routine d'intégration par la méthode Runge-Kutta du 4ème ordre.
forsythe.f90, un module qui contient les interfaces des sous-routines de Forsythe.
nrtype.f90, un module défini dans les Numerical Recipes.

rkf45.f90

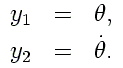
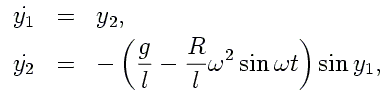
subroutine 
rkf45(f,neqn,y,t,tout,relerr,abserr,iflag,work,iwork)

rkf45 intègre un système de neqn équations différentielles du 1er ordre de la forme dy(i)/dt=f(t,y(1),...,y(neqn)) où les y(i) sont calculés en t.
t est la variable d'intégration et l'intégration se fait depuis la valeur initiale de t jusque tout.
f(t,y,yp) est une sous-routine qui fournit la valeur des dérivées premières yp(i) (valeurs de sortie) au point t pour des valeurs données des y(i) (valeurs d'entrée). y(1:neqn) et yp(1:neqn) sont donc des vecteurs qui contiennent respectivement les fonctions y_i ainsi que leur dérivée y'_i. Cette sous-routine doit être construite par l'utilisateur. Vous trouverez l'interface de cette sous-routine dans le code de rkf45.
abserr et relerr sont respectivement les erreurs absolues et relatives demandées par l'utilisateur. Prenez abserr=0. et relerr=1.E-8.
work est un vecteur réel utilisé par la routine, qui doit être de dimension 3+6*neqn.
iwork est un vecteur d'entiers, qui doit être de dimension 5.
iflag en entrée indique à la sous-routine ce qu'elle doit faire et en sortie ce qu'elle a fait.
En entrée:

iflag=1: si on veut intégrer entre la valeur initiale de t et tout en un seul appel à la sous-routine (c'est ce que l'on veut).
iflag=-1: si on ne veut effectuer qu'un seul pas d'intégration dans la direction de tout (ne pas utiliser cela).

En sortie:

iflag=2: indique que l'intégration continue s'est bien déroulée.
iflag=-2: indique que l'intégration d'un seul pas s'est bien déroulée.

Pour plus d'information, voir les commentaires au début de la routine rkf45.

Le tout est donc d'initialiser les valeurs de y₁=θ et y₂=θ' en t=0, et de faire appel à rkf45 pour propager ces valeurs sur la période de temps souhaitée.

Application

Pour fixer les choses, nous prenons l = 15 m et g=9.81 m/s². Dans l'approximation des angles petits, la fréquence propre du pendule non excité est donnée par:

La période naturelle d'oscillation du pendule est donc

qui vaut 7.769 s.

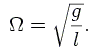
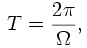
Nous allons étudier les oscillations du pendule sur une période de temps allant de t=0 jusque t=2.T. Vous prendrez 10.000 points intermédiaires.

Votre programme devra pouvoir représenter θ en fonction de t, θ' en fonction de t, ainsi que θ' en fonction de θ.

Voici les résultats à retrouver pour quatre situations différentes :

Mouvement propre: prenez R=0 m, ω=0 s^-1, θ(0)=0.05 et θ'(0)=0 s^-1 (résultats: θ-t ; θ'-θ).
Excitation lente: prenez R=0.5 m, ω=5.3 s^-1, θ(0)=0.05 et θ'(0)=0 s^-1 (résultats: θ-t ; θ'-θ).
Excitation rapide: prenez R=0.5 m, ω=100 s^-1, θ(0)=3.1 et θ'(0)=0 s^-1 (résultats: θ-t ; θ'-θ).
Excitation rapide et forte: prenez R=2 m, ω=100 s^-1, θ(0)=3.1 et θ'(0)=0 s^-1 (résultats: θ-t ; θ'-θ).

Pour votre rapport, vous me remettrez le graphique de θ'-θ pour le mouvement propre du pendule (premier cas) ainsi que le graphique de θ'-θ pour une excitation rapide et forte du pendule (quatrième cas).

Travaillez en double précision.

L'interface de rkf45 se trouve dans le module forsythe. Faites-y appel par: use forsythe, only: rkf45
Comme dit précédemment, prenez abserr=0. et relerr=1.E-8.
Mettez iflag = 1 en entrée et vérifiez en sortie que iflag = 2.

Voici le Makefile à utiliser avec le gfortran (le programme principal doit s'appeler Pendule.f90).

Remarque

Nous avons considéré 10.000 valeurs intermédiaires entre t=0 et 2.T dans le seul but de représenter graphiquement les valeurs de θ et θ' entre ces deux points. Si seules les valeurs en t=2.T avaient été demandées, on aurait pu propager θ et θ' de t=0 à 2.T en une seule étape (en prenant directement tout=2.T).