Les lois de Kirchhoff

Présentation et théorie

Considérons un réseau de résistances quelconques. Si on applique une tension V aux bornes de ce réseau, il présentera une résistance équivalente R', telle que le courant i aux bornes du générateur est donné par i=V/R'. Le calcul de cette résistance équivalente est relativement simple dans le cas de résistances en parallèle ou en série, mais peut être ardu pour un sytème plus complexe.

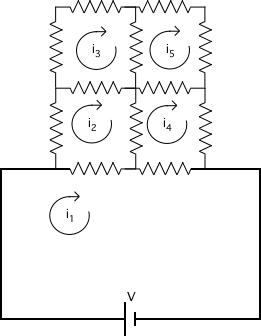
Pour résoudre ce type de problèmes, on fait appel à la théorie de Kirchhoff. On regarde le circuit comme un ensemble fini de boucles fermées dans lesquelles circule un courant (à déterminer). Pour chacune de ces boucles, on fait la somme des énergies dissipées dans les résistances de cette boucle, et on l'égale à la différence de potentiel à l'extrémité de la boucle (qui sera nulle partout, sauf pour la boucle passant par le générateur).

Prenons par exemple un circuit composé de 2x2 carrés où toutes les résistances sont égales.

Il présente 5 boucles, i₁...i₅. Le système est alors le suivant:
boucle 1: V=R(i₁-i₂) + R(i₁-i₄)
boucle 2: 0= Ri₂ + R(i₂-i₃) + R(i₂-i₄) + R(i₂-i₁)
boucle 3: 0= 2 Ri₃ + R(i₃-i₅) + R(i₃-i₂)
boucle 4: 0= Ri₄ + R(i₄-i₁) + R(i₄-i₂) + R(i₄-i₅)
boucle 5: 0= 2Ri₅ + R(i₅-i₄) + R(i₅-i₃)
Il peut se mettre sous forme d'une équation matricielle. La résolution de ce système se fait alors par les techniques standard de l'algèbre.

Mise en pratique

Nous allons considérer le système suivant:

Nous supposons que toutes les résistances R sont identiques et qu'une tension V est appliquée.

La première partie de l'exercice consiste à écrire le système d'équations correspondant à ce circuit et à le mettre sous la forme matricielle V = M.I, où V est un vecteur contenant les tensions appliquées aux bornes de chaque boucle et I un vecteur contenant les valeurs du courant dans ces mêmes boucles. Une fois la matrice M construite, les valeurs de courant peuvent s'obtenir formellement par I = M^-1.V et la résistance équivalente R' est donnée par R'=V/i₁, où i₁ est le courant dans la boucle passant par le générateur.

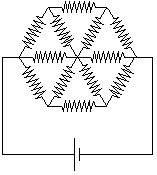
Le tout est donc de construire cette matrice M pour le circuit considéré et de résoudre le système V = M.I. Vous écrirez votre programme de manière à pouvoir traiter un système à N côtés, où N sera toujours égal ou supérieur à 4 (vous l'appliquerez cependant au cas N=6 pour commencer). Les connexions au générateur se feront toujours de manière symétrique comme indiqué sur la figure (attention aux cas où N est impair!). Pour obtenir la décomposition Gauss-Jordan de la matrice M, vous utiliserez la sous-routine decomp. Pour résoudre ensuite le système V = M.I, vous utiliserez la sous-routine solve. Vous trouverez au début de ces routines des explications sur leur utilisation. Notez que ipvt(1:N) et work(1:N) sont des vecteurs d'entiers et de réels respectivement. Les interfaces de ces sous-routines sont contenues dans le fichier forsythe.f90. Vous pouvez y faire référence en faisant use forsythe, only: decomp, solve. Vous avez également besoin de nrtype.f90.

Voici le Makefile à utiliser avec le gfortran (le programme principal doit s'appeler Kirchhoff.f90).

Une fois que le programme fonctionnera pour N=6, vous l'appliquerez à un nombre croissant de résistances. Pour chaque cas, vous calculerez la condition de la matrice (afin de vérifier la validité de vos résultats) ainsi que la résistance équivalente.