Interpolation

Présentation

Lors d'une expérience avec une cellule photoélectrique, on mesure le potentiel V en fonction du courant I. Les 14 points ainsi mesurés sont stockés dans le fichier cell.dat. En interpolant la tension V pour toutes les valeurs possibles du courant I, on se propose de déterminer pour quelle valeur du courant la puissance I.V est maximale.

Mise en pratique

Ce projet consiste en quatre étapes, à réaliser progressivement:

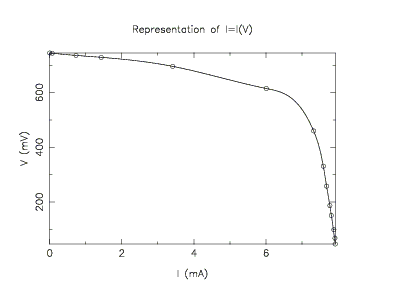
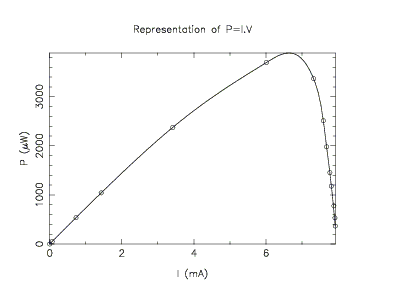
Commencez par lire le fichier cell.dat. Les valeurs du courant doivent être stockées dans un vecteur List_x(1:n) et les valeurs de la tension dans un vecteur List_y(1:n). n est ici le nombre de lignes dans le fichier cell.dat.
En se servant de spline et splint, vous allez ensuite interpoler la courbe y(x) qui passe par les points lus précédemment. Vous représenterez le résultat de cette interpolation sur une centaine de points compris entre List_x(1) et List_x(n).
L'étape suivante consiste à construire une fonction func(x) qui calcule la puissance I.V pour un courant x quelconque. Comme dans l'étape précédente, cette fonction utilisera splint. x étant le seul argument permis pour func(x), vous transmettrez les autres informations nécessaires via un module donnees_communes. Une fois réalisée, vous représenterez cette fonction func(x) sur une centaine de points entre List_x(1) et List_x(n).
La dernière étape consiste à chercher le maximum de cette courbe de puissance. Vous utiliserez pour cela la fonction golden et chercherez le minimum d'une fonction func(x) modifiée donnant -I.V.

Sous-routines

Les routines et modules nécessaires sont:

Ces sous-routines et fonctions marchent en simple précision. Tout le programme doit donc être écrit en simple précision (r=4 ou SP).
Le module nr.f90 contient les interfaces de toutes les sous-routines et fonctions du Numerical Recipes de sorte qu'il n'est pas nécessaire de les recréer dans le module list_interface. On les invoque en faisant, dans le programme principal par exemple,
use nr, only: spline, splint, golden.
La fonction func(x), qui sera minimisée par golden.f90, doit être créée explicitement et son interface également présente dans list_interface. Comme dit précédemment, les paramètres dont la fonction func(x) peut avoir besoin, en dehors de x lui-même, doivent être passés par un module donnees_communes (cfr exemple).

Voici le Makefile à utiliser avec le gfortran (le programme principal doit s'appeler Interpolation.f90).

spline.f90

subroutine spline(List_x,List_y,yp1,ypn,List_y2)

Etant donnés deux vecteurs de même dimension List_x(1:n) et List_y(1:n), ainsi que les dérivées premières yp1 et ypn en List_x(1) et List_x(n), la sous-routine renvoie un vecteur List_y2(1:n) qui contient les dérivées secondes de la fonction en chaque point. Pour obtenir une spline naturelle (dérivée seconde nulle aux extrémités), vous prendrez yp1=ypn=1.E30_4.

splint.f90

function splint(List_x,List_y,List_y2,x)

Etant donnés trois vecteurs de même dimension List_x(1:n), List_y(1:n) et List_y2(1:n) qui reprennent respectivement les abscisses, les ordonnées et les dérivées secondes d'une fonction échantillonnée, y=splint(List_x,List_y,List_y2,x) interpole la fonction au point x.

golden.f90

function golden(a,b,c,func,tol,xmin)

Cette fonction recherche le minimum entre a et c d'une fonction func(x) à une seule variable x.

Il faut lui fournir le nom de la fonction func à minimiser ainsi que les points a, b et c. Ceux-ci sont choisis de telle sorte que a < b < c et que func(b) soit inférieur à func(a) et func(c). La fonction golden utilise la méthode golden search et renvoit le minimum de la fonction func(x). L'incertitude absolue sur x est spécifiée par tol (prenez tol=1.E-7_4). L'abscisse du minimum trouvé est retournée dans xmin.