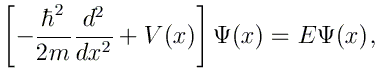
Calcul des états liés d'un potentiel harmonique

Théorie

Nous allons résoudre cette fois l'équation de Schrödinger indépendante du temps:

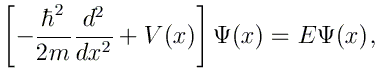
où tous les symboles ont leur signification habituelle en mécanique quantique.

Cette équation peut être discrétisée comme

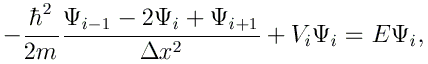
où les quantités indicées par i correspondent à des valeurs de x espacées de Δx. Nous considérons un système de longueur L et des indices i allant de 0 à N (Δx=L/N). Comme précédemment, nous posons comme conditions frontières que Ψ0=ΨN=0.

Les équations obtenues pour i allant de 1 à N-1 peuvent alors se mettre sous la forme matricielle

où
On se trouve donc face à un système du type Ax=λx, où la matrice A est tridiagonale. Nous utiliserons la sous-routine dstevd de LAPACK pour calculer les valeurs et vecteurs propres de la matrice A. Cette résolution fournira l'énergie E et la fonction d'onde Ψ des N-1 premiers états liés du potentiel V.

Mise en pratique

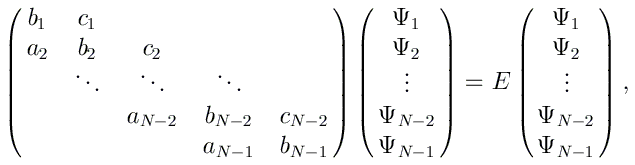
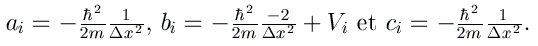
Nous allons calculer les états liés du potentiel harmonique

où k= 2.102601586267. Cette dernière valeur a été choisie de manière à obtenir
Le système considéré ira de x0=-L/2 à xN=L/2, où l'on force la fonction d'onde à s'annuler.

  1. Vous allez considérer dans un premier temps des valeurs de x allant de x0=-15 Å à xN= 15 Å. Vous prendrez N=150 (Δx=0.2 Å).
    En appliquant la théorie développée précédemment, calculez l'énergie et la fonction d'onde des 5 premiers états liés.

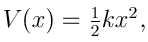
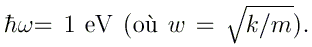
    Les niveaux d'énergie sont-ils en accord avec la formule

    Vous représenterez la fonction d'onde de ces états avec le programme GetPlot.

  2. En comparant vos résultats numériques avec la formule analytique, calculez l'erreur relative sur les 100 premiers niveaux d'énergie.
    Vous représenterez cette erreur de manière graphique.

  3. Afin d'observer l'influence des conditions frontières, vous allez considérer ensuite des x allant de x0=-30 Å à xN= 30 Å.
    Vous prendrez N=300 de manière à conserver Δx=0.2 Å.
    Recalculez l'erreur relative sur les 100 premiers niveaux d'énergie.

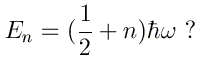
    Comment expliquez-vous la différence avec le résultat précédent ?

    Pour vous aider à répondre à cette question, vous allez comparer la fonction d'onde associée avec le vingtième état lié, telle qu'obtenue avec des frontières situées à 15 Å et 30 Å du centre.
    Commentez l'impact des conditions frontières sur ce résultat.

  4. Afin d'observer l'influence de la résolution (pas Δx), vous allez considérer des x allant de x0=-30 Å à xN= 30 Å en prenant cette fois N=600 (Δx=0.1 Å).
    Recalculez l'erreur relative sur les 100 premiers niveaux d'énergie.
    Quelle différence y a-t-il par rapport au cas précédent ?

    Pour le rapport, vous représenterez les trois courbes d'erreur sur le même graphique.

  5. Vous allez finalement appliquer la technique des fractions continues pour vérifier que l'on peut effectivement retrouver les niveaux d'énergie des états liés à partir des racines de cette fraction.

    L'équation de Schrödinger que nous cherchons à résoudre peut en effet se mettre sous la forme

    où
    Puisque nous posons ΨN=0, nous avons RN-1=∞ de sorte que RN-2=bN-1. Nous pouvons alors écrire
    Les énergies E des états liés sont celles qui vérifient R0(E)=0.

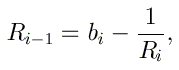
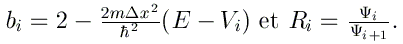
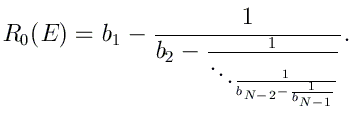
    En utilisant les relations données dans Abramowitz, on peut montrer que

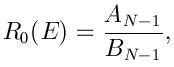
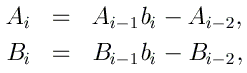
    où les coefficients Ai et Bi obéissent aux relations de récurence
    avec A0=1, A1=b1, B0=0 et B1=1 comme conditions initiales.

    En calculant AN-1(E) pour 10000 valeurs entre 0 et 10 eV, vous allez vérifier graphiquement que les racines de AN-1(E) correspondent effectivement aux énergies des états liés du potentiel harmonique. Vous représenterez |AN-1(E)| en échelle logarithmique. Travaillez ici avec N=150 et des x allant de x0=-15 Å à xN= 15 Å.

A remettre ...

Pour ce TP, vous devez me remettre:

Sous-routine DSTEVD pour calculer les valeurs et vecteurs propres d'une matrice symmétrique tridiagonale réelle

Pour calculer les valeurs et vecteurs propres d'une matrice symmétrique tridiagonale réelle (double précision), vous pouvez utiliser la sous-routine dstevd de la librairie LAPACK. Sa syntaxe est la suivante:

call dstevd( JOBZ, N, D, E, Z, LDZ, WORK, LWORK, IWORK, LIWORK, INFO )

où JOBZ='V' pour obtenir les valeurs et vecteurs propres, N et LDZ spécifient l'ordre de la matrice à diagonaliser, D(1:N) est un vecteur qui contient les éléments diagonaux de cette matrice, E(1:N) est un vecteur qui contient dans ses N-1 premières composantes les éléments sous-diagonaux de la matrice, Z(1:N,1:N) est une matrice qui contient en sortie les vecteurs propres de la matrice (ils sont rangés en colonnes), WORK(1:LWORK) est un espace de travail (il s'agit d'un vecteur réel double précision), LWORK=1+4*N+N**2, IWORK(1:LIWORK) est un autre espace de travail (il s'agit d'un vecteur entier), LIWORK=3+5*N et INFO est un entier qui vaut 0 en sortie si tout s'est bien passé. En sortie de la sous-routine, les valeurs propres de la matrice sont rangées par ordre croissant dans le vecteur D(1:N). Vous trouvez toutes ces explications au début du listing de dstevd.

Vous pouvez utiliser dstevd directement, sans l'inclure dans votre projet ni créer d'interface ! Il faut cependant compiler votre projet en le liant à la librairie LAPACK. La manière de faire dépend de votre compilateur. Vous trouverez les explications nécessaires sur ma page consacrée à LAPACK. On trouve facilement la routine à utiliser pour un problème donné en parcourant le site de la librairie. La manière d'utiliser cette routine est alors expliquée au début du listing.

Sous-routine Plot pour une représentation graphique de fonctions y=y(x)

Afin de représenter graphiquement vos résultats, vous pouvez utiliser la routine Plot. Celle-ci vous permet de visualiser une ou plusieurs fonctions y=y(x) en faisant simplement call Plot(list_x, list_y). Vous devez pour cela inclure use PlotPack dans les parties de vos programmes qui utilisent Plot. Vous trouverez plus de détails sur son utilisation dans les commentaires préliminaires du fichier.

Programme Plot.py pour une représentation graphique de fonctions y=y(x)

Si vous connaissez le Python, vous pouvez également faire python Plot.py Plot.dat (Python 2.7). Vous trouverez dans le fichier Plot.dat un exemple de format à respecter.

Programme GetPlot pour une représentation graphique de fonctions y=y(x)

Afin de représenter graphiquement vos résultats et produire des fichiers PostScript, vous pouvez utiliser le programme GetPlot.exe. Celui-ci vous permet de visualiser une ou plusieurs fonctions y=y(x), en exécutant simplement ce programme dans le répertoire où se trouvent vos fichiers. Le lien suivant décrit le format des fichiers de données.