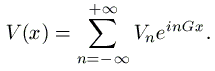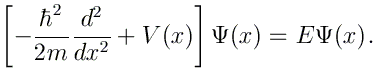
Calcul de la structure de bandes d'un potentiel périodique

Théorie pour un calcul de structures de bandes par différences finies

Nous résolvons toujours l'équation de Schrödinger indépendante du temps

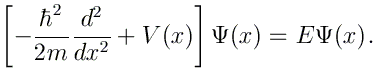
Le potentiel V est cette fois périodique et vérifie donc V(x+L) = V(x), où L est la longueur du motif périodique.

D'après le théorème de Bloch, la fonction d'onde peut s'exprimer comme Ψ(x)=u(x) e^ikx, où u(x+L)=u(x) et k est le vecteur d'onde.

Nous pouvons donc poser

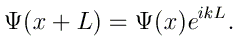
En pratique, les valeurs de ce vecteur d'onde k sont restreintes à la première zone de Brillouin [-π/L, π/L]. Pour obtenir la structure de bandes de ce système, il faut en fait calculer les valeurs de l'énergie E en fonction du vecteur d'onde k.

Il est possible d'obtenir cette structure de bandes par différences finies. L'équation de Schrödinger peut en effet se discrétiser comme

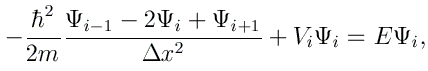
où les quantités indicées par i correspondent à des valeurs en x=i.Δx (Δx=L/N). Nous travaillerons avec des indices i allant de 1 à N.

Nous utilisons cette fois comme conditions frontières

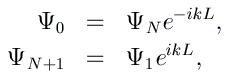
où k est choisi dans la première zone de Brillouin [-π/L, π/L]. Ψ_N n'est donc pas trivialement nul et doit être calculé au même titre que Ψ₁, Ψ₂, etc.

Les équations obtenues pour i allant de 1 à N peuvent alors se mettre sous la forme

où

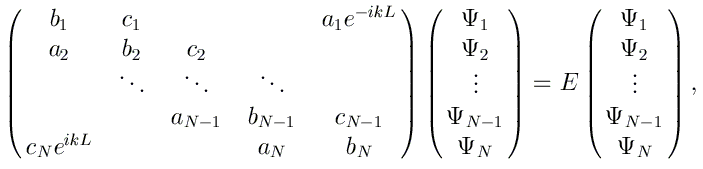
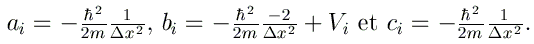
On se trouve à nouveau face à un système du type Ax=λx. Pour une valeur donnée de k, les valeurs propres de la matrice A fournissent donc les énergies E(k). Les vecteurs propres fournissent quant-à-eux les amplitudes de la fonction d'onde Ψ_k dans l'intervalle [0, L]. La matrice A n'est cependant plus tridiagonale. Pour la diagonaliser, nous utiliserons la sous-routine zheevd de LAPACK.

Mise en pratique

Nous allons calculer la structure de bandes associée au potentiel

où V₁ = 1 eV et L = 0.4336 nm.

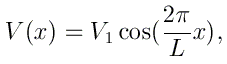
Prenez N=40 points pour discrétiser le motif périodique [0, L]. Vous échantillonerez la première zone de Brillouin [-π/L, π/L] en prenant des k espacés de (1/1000) 2π/L. Pour chaque valeur de k, vous calculerez les niveaux d'énergie E(k). L'exercice consiste à représenter la structure de bandes E=E(k) du cristal (ne représentez que les énergies E(k) qui sont en deçà de 10 eV).

Vos résultats se présenteront sous la forme de points dispersés. Vous les représenterez en utilisant la libriairie PGPLOT. La représentation graphique devra se faire dans un programme séparé. Les calculs doivent se faire en double précision. Convertissez vos résultats en simple précision pour les représenter avec PGPLOT.

Théorie pour un calcul de structures de bandes par ondes planes

Les structures de bandes sont plus souvent calculées en utilisant une représentation par ondes planes. L'énergie potentielle V(x) considérée précédemment s'écrit dans cette représentation comme

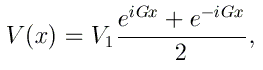
où G=2π/L. Cette écriture n'est rien d'autre qu'un développement en séries de Fourier de V(x). ¹

En se basant à nouveau sur le théorème de Bloch, on peut développer la fonction d'onde Ψ(x) comme

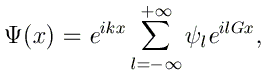
où les coefficients ψ_l dépendent de k.

En remplaçant ces expressions de V(x) et Ψ(x) dans l'équation de Schrödinger

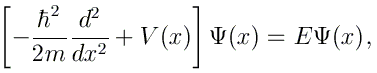
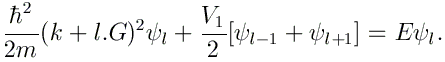
on montre facilement que les coefficients ψ_l obéissent à l'équation

Les équations obtenues en considérant des indices l allant de -N à +N peuvent alors se mettre sous la forme

où

La structure de bandes E=E(k) s'obtient alors comme précédemment en calculant les valeurs propres de cette matrice.

Mise en pratique

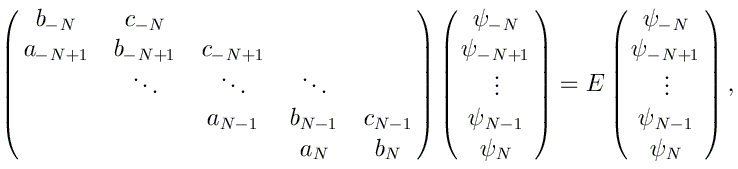
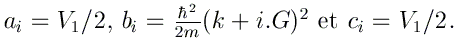
Nous allons calculer la structure de bandes associée au potentiel V(x) par cette deuxième méthode. Comme précédemment, la première zone de Brillouin [-π/L, π/L] sera échantillonée avec des k espacés de (1/1000) 2π/L et vous ne conserverez que les valeurs de E(k) qui sont en deçà de 10 eV.

Vous appliquerez cette deuxième technique en prenant N=2 (notez l'économie dans la représentation!) et superposerez la structure de bandes ainsi obtenue avec le résultat précédent (prenez une autre couleur).

L'accord entre les deux techniques est-il satisfaisant ?

Observez ce qu'il se passe lorsqu'on applique la méthode par différences finies avec N=10, 20 et 40 points de discrétisation.

Observez ce qu'il se passe lorsqu'on applique la méthode par ondes planes avec N=0, 1 et 2. Comment expliquez-vous le résultat obtenu avec N=0?

A remettre ...

Pour ce TP, vous devez me remettre:

le listing de vos deux programmes (structure de bandes par les deux méthodes + représentation graphique)
la structure de bandes, telle qu'obtenue par différences finies (pour N=10, 20 et 40 points de discrétisation) et ondes planes (pour N=2) [3 graphiques]
la structure de bandes, telle qu'obtenue par différences finies (pour N=40 points de discrétisation) et ondes planes (pour N=0) [1 graphique]
vos réponses aux questions

Sous-routine ZHEEVD pour calculer les valeurs et vecteurs propres d'une matrice hermitienne complexe

Pour calculer les valeurs et vecteurs propres d'une matrice hermitienne complexe (double précision), vous pouvez utiliser la sous-routine zheevd de la librairie LAPACK. Sa syntaxe est la suivante:

call ZHEEVD( JOBZ, UPLO, N, A, LDA, W, WORK, LWORK, RWORK, LRWORK, IWORK, LIWORK, INFO )

où JOBZ='N' pour obtenir les valeurs propres (sans les vecteurs propres), UPLO='U' pour indiquer que l'on fournit la partie triangulaire supérieure de la matrice, N et LDA spécifient l'ordre de la matrice à diagonaliser, A(1:N,1:N) est la matrice complexe à diagonaliser, W(1:N) est un vecteur réel double précision qui contient en sortie les valeurs propres, WORK(1:LWORK) est un vecteur complexe double précision (espace de travail), LWORK=N+1, RWORK(1:LRWORK) est un vecteur réel double précision (espace de travail), LRWORK=N, IWORK(1:LIWORK) est un vecteur entier (espace de travail), LIWORK=1 et INFO est un entier qui vaut 0 en sortie si tout s'est bien passé. En sortie de la sous-routine, les valeurs propres de la matrice sont rangées par ordre croissant dans le vecteur W(1:N). Vous trouvez toutes ces explications au début du listing de zheevd.

Vous pouvez utiliser zheevd directement, sans l'inclure dans votre projet ni créer d'interface ! Il faut cependant compiler votre projet en le liant à la librairie LAPACK. La manière de faire dépend de votre compilateur. Vous trouverez les explications nécessaires sur ma page consacrée à LAPACK. On trouve facilement la routine à utiliser pour un problème donné en parcourant le site de la librairie. La manière d'utiliser cette routine est alors expliquée au début du listing.

Sous-routine Plot pour une représentation graphique de fonctions y=y(x)

Afin de représenter graphiquement vos résultats, vous pouvez utiliser la routine Plot. Celle-ci vous permet de visualiser une ou plusieurs fonctions y=y(x) en faisant simplement call Plot(list_x, list_y). Vous devez pour cela inclure use PlotPack dans les parties de vos programmes qui utilisent Plot. Vous trouverez plus de détails sur son utilisation dans les commentaires préliminaires du fichier.

Programme Plot.py pour une représentation graphique de fonctions y=y(x)

Si vous connaissez le Python, vous pouvez encore faire python Plot.py Plot.dat (Python 2.7). Vous trouverez dans le fichier Plot.dat un exemple de format à respecter.

Programme GetPlot pour une représentation graphique de fonctions y=y(x)

Afin de représenter graphiquement l'énergie potentielle et produire un fichier PostScript, vous pouvez utiliser le programme GetPlot.exe. Celui-ci vous permet de visualiser une ou plusieurs fonctions y=y(x), en exécutant simplement ce programme dans le répertoire où se trouvent vos fichiers. Le lien suivant décrit le format des fichiers de données.

¹ D'une manière plus générale, on peut en effet exprimer l'énergie potentielle V(x) comme